二叉树的定义
二叉树(Binary Tree):树中各个节点的度不大于 2 个的有序树,称为二叉树。通常树中的分支节点被称为 「左子树」 或 「右子树」。二叉树的分支具有左右次序,不能随意互换位置。
二叉树也可以使用递归方式来定义,即二叉树满足以下两个要求之一:
- 空树:二叉树是一棵空树。
- 非空树:二叉树是由一个根节点和两棵互不相交的子树
、 ,分别称为根节点的左子树、右子树组成的非空树;并且 、 本身都是二叉树。
⼆叉树是种特殊的树,它最多有两个子树,分别为左子树和右子树,并且两个子树是有序的,不可以互换。也就是说,在⼆叉树中不存在度大于 2 的节点。
二叉树在逻辑上可以分为 5 种基本形态,如下图所示。

特殊的二叉树
斜树
所有结点都只有左子树的二叉树,被称为左斜树,像这样:

所有结点都只有右子树的二叉树,被称为右斜树,像这样:

满二叉树
满二叉树(Full Binary Tree):如果所有分支节点都存在左子树和右子树,并且所有叶子节点都在同一层上,则称该二叉树为满二叉树。
满二叉树满足以下特点:
- 叶子节点只出现在最下面一层。
- 非叶子节点的度一定为 2。
- 在同等深度的二叉树中,满二叉树的节点个数最多,叶子节点个数最多。
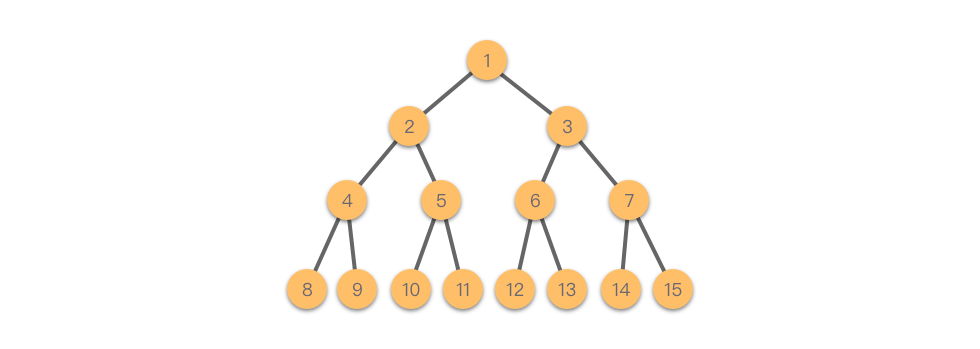
如果我们对满二叉树的节点进行编号,根节点编号为 1,然后按照层次依次向下,每一层从左至右的顺序进行编号。则深度为

完全二叉树
对一棵具有 n 个结点的二叉树,按照层序进行编号,如果编号
完全二叉树满足以下特点:
- 叶子节点只能出现在最下面两层。
- 最下层的叶子节点一定集中在该层最左边的位置上。
- 倒数第二层如果有叶子节点,则该层的叶子节点一定集中在右边的位置上。
- 如果节点的度为 1,则该节点只偶遇左孩子节点,即不存在只有右子树的情况。
- 同等节点数的二叉树中,完全二叉树的深度最小。
完全二叉树可以使用类似满二叉树的节点编号的方式来定义。即从根节点编号为

二叉树的性质
二叉树的第
( )层上最多 个结点; 归纳法证明:
归纳假设:
- 假设对于某个
,二叉树最多有 个结点。
归纳步骤:
- 当
时,二叉树第一层只有根结点,结点数为1。 ,假设成立。 - 当
时,根据假设第 层最多有 个结点。因为每个结点最多有2个孩子结点,因此第 层最多有 个结点。 满足假设。
结论:
- 通过数学归纳法,性质对于所有
成立。
- 假设对于某个
深度为
的二叉树至多 个结点; 证明:
根据性质1,可知二叉树的第
层最多有 个结点,深度为 的二叉树层数为 到 。 因此总结点上限满足:
因此结论成立,得证。
若在任意一棵二叉树中,有
个叶子节点,有 个度为 的节点,则必有 ; 证明:
性质相关公式:
- 二叉树总结点数公式:
其中,
是总结点数, 是度为1的结点数, 是度为2的结点数。 - 度数公式:
在一棵二叉树中,总边数为(因为除根节点外,每个节点都有一个父节点)。
每个度为1的节点贡献1条边,每个度为2的节点贡献2条边。
因此:
联立方程求解:
用方程(1)减去方程(2):
化简得:
结论成立
个结点的完全二叉树的深度为 (其中 代表对 取下整); 证明:
深度为
的完全二叉树的结点数满足: 对数变换得:
实际上,为了简化分析,可以近似认为:
对
取下整(即向下取整),得到的整数部分是 : 因此,深度h等于:
结论成立。
若对一棵有
个节点的完全二叉树进行顺序编号( ),那么,对于编号为 ( )的节点:(以下为索引0留空的) 当
时,该节点为根,它无双亲节点。 当
时,该节点的双亲节点的编号为 。 若
,则有编号为 的左节点,否则没有左节点。 若
,则有编号为 的右节点,否则没有右节点。
二叉树的存储结构
二叉树的存储结构分为两种:「顺序存储结构」和「链式存储结构」。
二叉树的顺序存储结构
堆排序、优先队列中的二叉堆结构,采用的就是二叉树的顺序存储结构。
二叉树的顺序存储结构使用一维数组来存储二叉树中的节点,节点存储位置则采用完全二叉树的节点层次编号,按照层次从上至下,每一层从左至右的顺序依次存放二叉树的数据元素。在进行顺序存储时,如果对应的二叉树节点不存在,则设置为「空节点」。
下图为二叉树的顺序存储结构。

在索引0不留空得情况下,结点编号满足
- 如果某二叉树节点(非叶子节点)的下标为
,那么其左孩子节点下标为 ,右孩子节点下标为 。 - 如果某二叉树节点(非根节点)的下标为
,那么其父节点下标为 。
有时候为了方便也直接把顺序表索引为0的位置留空。
对于完全二叉树(尤其是满二叉树)来说,采用顺序存储结构比较合适,它能充分利用存储空间;而对于一般二叉树,如果需要设置很多的「空节点」,则采用顺序存储结构就会浪费很多存储空间。并且,由于顺序存储结构固有的一些缺陷,会使得二叉树的插入、删除等操作不方便,效率也比较低。对于二叉树来说,当树的形态和大小经常发生动态变化时,更适合采用链式存储结构。
二叉树的链式存储结构
二叉树采用链式存储结构时,每个链节点包含一个用于数据域

下面我们将值为

二叉树的链表存储结构具有灵活、方便的特点。节点的最大数目只受系统最大可存储空间的限制。一般情况下,二叉树的链表存储结构比顺序存储结构更省空间(用于存储指针域的空间开销只是二叉树中节点数的线性函数),而且对于二叉树实施相关操作也很方便,因此,一般我们使用链式存储结构来存储二叉树。
二叉树的遍历概念
二叉树的遍历:指的是从根节点出发,按照某种次序依次访问二叉树中所有节点,使得每个节点被访问一次且仅被访问一次。
对于线性表的遍历,要么从头到尾,要么从尾到头,遍历方式较为单纯。但是树不一样,它的每个结点都有可能有两个孩子结点,所以遍历的顺序面临着不同的选择。
二叉树的前序遍历
二叉树的前序遍历规则为:
- 如果二叉树为空,则返回。
- 如果二叉树不为空,则:
- 访问根节点。
- 以前序遍历的方式遍历根节点的左子树。
- 以前序遍历的方式遍历根节点的右子树。
从二叉树的前序遍历规则可以看出:前序遍历过程是一个递归过程。在遍历任何一棵子树时仍然是按照先访问根节点,然后遍历子树根节点的左子树,最后再遍历子树根节点的右子树的顺序进行遍历。
如下图所示,该二叉树的前序遍历顺序为:

二叉树的中序遍历
二叉树的中序遍历规则为:
- 如果二叉树为空,则返回。
- 如果二叉树不为空,则:
- 以中序遍历的方式遍历根节点的左子树。
- 访问根节点。
- 以中序遍历的方式遍历根节点的右子树。
从二叉树的中序遍历规则可以看出:中序遍历过程也是一个递归过程。在遍历任何一棵子树时仍然是按照先遍历子树根节点的左子树,然后访问根节点,最后再遍历子树根节点的右子树的顺序进行遍历。
如下图所示,该二叉树的中序遍历顺序为:

二叉树的后序遍历
二叉树的后序遍历规则为:
- 如果二叉树为空,则返回。
- 如果二叉树不为空,则:
- 以后序遍历的方式遍历根节点的左子树。
- 以后序遍历的方式遍历根节点的右子树。
- 访问根节点。
从二叉树的后序遍历规则可以看出:后序遍历过程也是一个递归过程。在遍历任何一棵子树时仍然是按照先遍历子树根节点的左子树,然后遍历子树根节点的右子树,最后再访问根节点的顺序进行遍历。
如下图所示,该二叉树的后序遍历顺序为:

二叉树的层序遍历
二叉树的层序遍历规则为:
- 如果二叉树为空,则返回。
- 如果二叉树不为空,则:
- 先依次访问二叉树第 11 层的节点。
- 然后依次访问二叉树第 22 层的节点。
- ……
- 依次下去,最后依次访问二叉树最下面一层的节点。
从二叉树的层序遍历规则可以看出:遍历过程是一个广度优先搜索过程。在遍历的时候是按照第 11 层、第 22 层、…… 最后一层依次遍历的,而同一层节点则是按照从左至右的顺序依次访问的。
如下图所示,该二叉树的后序遍历顺序为:

